Themen 2023

A) Rätselreise um die Welt
Kerstin Diesing, Fiona Höcker

Die Schülerinnen und Schüler begaben sich auf eine Rätselreise um die Welt. In vielen Rätseln, die man aus dem Alltag kennt, steckt ganz viel Mathematik. In diesem Projekt beschäftigten sich die Schülerinnen und Schüler mit verschiedenen Rätseln aus aller Welt (z. B. Hanjic, Sudoku, Kakuro, Kalaha, Somawürfel, Tangram). Sie lösten leichte bis sehr komplexe Rätsel und erarbeiteten dabei hilfreiche Lösungsstrategien. Auch mit dem Erstellen eigener Rätsel, Additionstürmen und Somawürfeln setzten sie sich auseinander. Am Ende waren alle aus der Gruppe wahre Rätselmeister!

B) Strichcodes - Das Geheimnis der Zebrastreifen
Saskia Busse, Klaus Porr

Zebras haben sie, auf der Straße sieht man sie – Muster aus schwarzen und weißen Streifen. Kaum beachtet, aber enorm wichtig, sind die schwarzen und weißen Striche auf allen Produkten, die man im Supermarkt kaufen kann. Sie sorgen dafür, dass Kassiererinnen und Kassierer keine Zahlen mehr eintippen müssen. Name und Preis des Produkts erscheinen wie durch Zauberei auf dem Kassenzettel.

Unsere Gruppe beschäftigte sich mit dem EAN-Code, der den Zebrastreifen zugrunde lag. Wie hingen die Striche mit den Ziffern zusammen? Warum war es egal, in welcher Richtung man das Produkt über den Warenscanner zog? Warum waren die Striche unterschiedlich dick, einige von ihnen länger, einige kürzer? Welche Zahl bedeutete was? Gibt es einen Unterschied zwischen Produkten, die in unterschiedlichen Ländern hergestellt wurden? Wie konnte man einen gefälschten Code entdecken und so den gemeinen Produktfälscherring entlarven, der unsere Stadt unsicher machte?

C) Alles geheim? - Macht nix! Geheimschriften entschlüsseln
Angelika Mertens, Sabine Reintges

In der Geschichte gab es viele Geheimschriften, weil wichtige Nachrichten verschlüsselt wurden. Die Angreifer haben natürlich versucht, den Code zu knacken und so galt eine Geheimschrift nur so lange als sicher, wie sie nicht geknackt wurde.
Die Projektgruppe erforschte verschiedene Verschlüsselungs- und Entschlüsselungstechniken.

D) Ganz besondere Körper: Platonische sowie archimedische Körper 
Antonia Kaiser, Henrik Bäumer

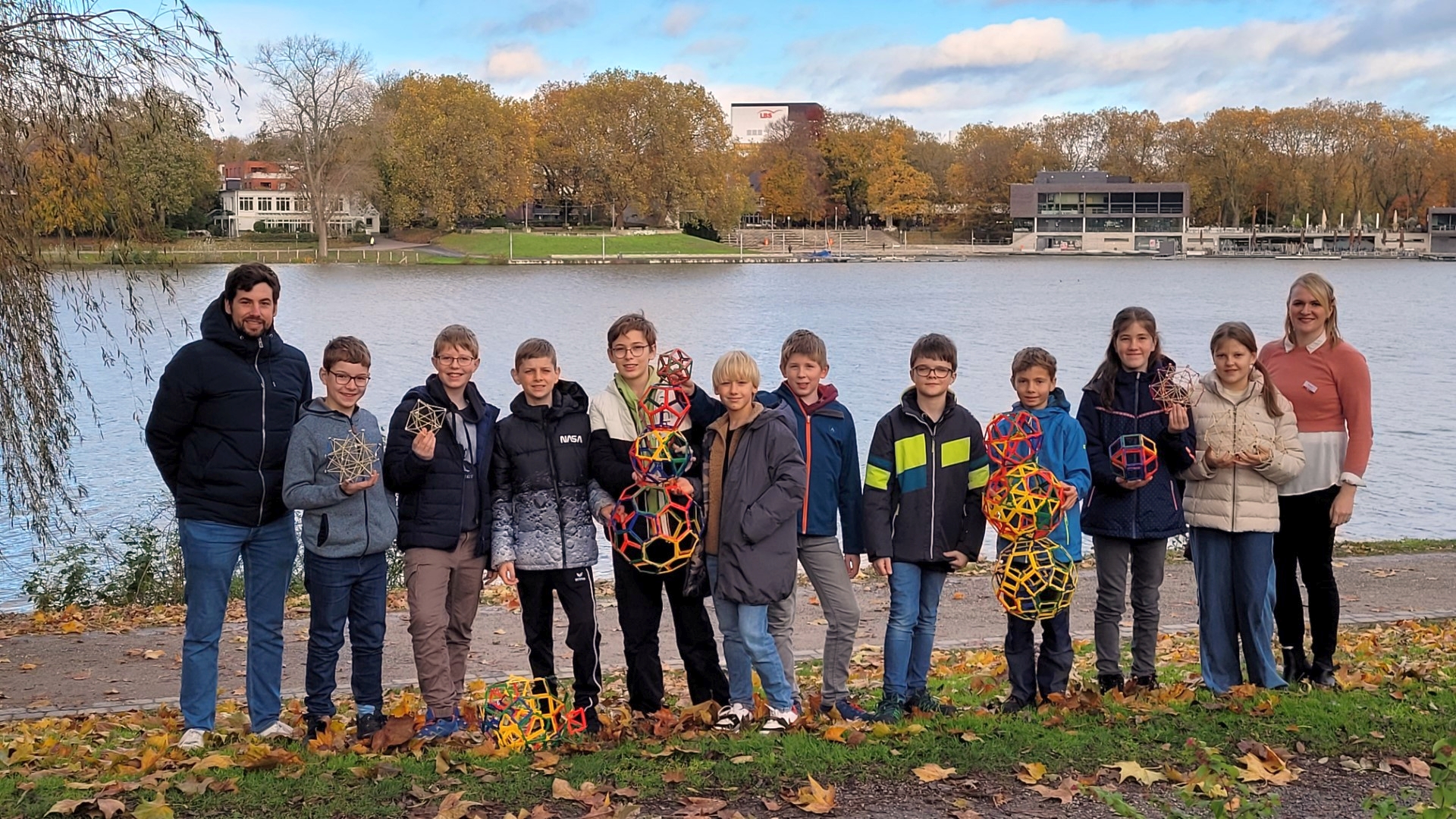
In dieser Gruppe ging es um ganz besondere Körper:
Platonische sowie archimedische Körper.
Was daran besonders ist und wie viele verschiedene es davon gibt, haben wir gemeinsam mithilfe von Erbsen, Zahnstochern und Clickies erkundet. 
Das mühsame Zählen von Ecken, Kanten und Flächen haben wir uns durch das Erarbeiten des Eulerschen Polyedersatzes erleichtert. Weitere Hausmittel in Form von Bohnen und Wollfäden haben uns geholfen, die Dualität der platonischen Körper zu entdecken. Absolutes Teamwork war dann beim Höhepunkt, dem Bauen der Sierpinski Pyramide, gefragt.

E) Programmierung von 3D-Geometrie-Modellen für AR- und 3D-Druck-Systeme
Julia Aldehoff, Hendrik Büdding

Mit Hilfe der Mathematik und Informatik wurde der Frage nachgegangen, wie aus einem 2D-Stadtplan ein 3D-Gebäude im Computer wird und wie es dann in AR dargestellt oder in einem 3D-Drucker ausgedruckt werden kann. Dabei halfen Informationen aus dem Internet und die Software Google-Earth. Hier bestand die Möglichkeit, nicht nur die Entfernung zwischen den einzelnen Gebäuden metergenau zu bestimmen, sondern auch deren Breite & Höhe & Tiefe.

Ausgewählte Gebäude wurden auf diese Weise untersucht, mithilfe von einer speziellen Block-Programmierumgebung programmiert und dann durch einen 3D-Drucker maßstabsgenau ausgedruckt. Wie das programmiert und wie der Ausdruck real erstellt wurde, wurde hier erforscht und an praktischen Beispielen durchgeführt.

Die Software, die für die Programmierung der Gebäude verwendet wurde, war BlockSCAD3D. Diese Software ermöglichte es, die Gebäude in 3D zu modellieren und sie dann in eine Datei zu exportieren, die von AR-Systemen und 3D-Drucker gelesen werden konnte. Die Gebäude wurden dann maßstabsgenau ausgedruckt, so dass sie exakt den Abmessungen entsprachen, die in der Software angegeben waren.